Artykuł obejmuje następujące tematy:
Zależności długości fal korekcyjnych i impulsowych według Prechtera. Zależności między zniesieniami, falami naprzemiennymi i falami zbieżnymi
Drodzy przyjaciele!
Dzisiaj zajmę się analizą proporcji opartą na geometrii Fibonacciego. Ta metoda nie powinna być używana jako niezależne narzędzie prognostyczne. Doskonale uzupełnia jednak opisane wcześniej wytyczne dotyczące zasady fali.
Jeśli nie znacie moich poprzednich artykułów poświęconych temu tematowi, polecam przeczytanie poniższych artykułów.
Teoria fal Elliotta według Billa Williamsa (Część 1 i Część 2),
Teoria fal Elliotta według Roberta Prechtera (Część 1 i Część 2, Część 3, Część 4).
Poza tym współczynniki (proporcje) wraz z innymi narzędziami analitycznymi można wykorzystać do przewidywania poziomów oporu, w przypadku których tendencja najprawdopodobniej ulegnie zmianie.
Wprowadzenie do geometrii Fibonacciego
Ciąg Fibonacciego 0, 1, 1, 2, 3, 5, 8… został odkryty przez Leonarda Fibonacciego z Pizy, wielkiego matematyka z XIII wieku. Pierwotnie ciąg ten był odpowiedzią na pytanie, ile królików może spłodzić para tych zwierząt rocznie, jeśli zostanie ona zamknięta w ograniczonym miejscu. Okazało się, że wielki matematyk odkrył uniwersalną sekwencję zachodzącą w wielu naturalnych obiektach i procesach.
W ciągu Fibonacciego każda następna liczba jest sumą dwóch poprzednich sąsiednich liczb. Inną ważną właściwością ciągu Fibonacciego jest stosunek dowolnej liczby do następnej wyższej wynoszącej około 0,618 do 1, i do następnej niższej liczby wynoszącej około 1,618 do 1, z wyjątkiem kilku pierwszych liczb w ciągu. Jest to tak zwana liczba φ (fi), która stała się podstawą Złotego Podziału lub Złotej Proporcji.
Dowolną długość można podzielić w taki sposób, aby stosunek części mniejszej do części większej był równy stosunkowi części większej do całości i wynosił 0,618. W naturze stosunek ten można znaleźć w różnych aspektach, strukturach atomowych i spiralach DNA, układach planetarnych i galaktykach. Złoty Podział jest wykorzystywany w architekturze, malarstwie, muzyce.
Bardziej złożonym obiektem opartym na liczbie φ jest złoty prostokąt, którego boki są w proporcji 1,618 do 1, czyli w którym stosunek dłuższego boku do krótszego jest równy złotej proporcji. Aby go skonstruować, należy najpierw narysować kwadrat o wymiarach 2x2, wewnątrz kwadratu narysować trójkąt z dwoma bokami wynoszącymi 2 i 1. Następnie przedłużyć krótszy bok tak, aby był równy pierwiastkowi kwadratowemu z 5 lub około 2,236 jednostek długości.
Bardziej skomplikowanym obiektem jest Złota Spirala, zbudowana jest za pomocą Złotego Prostokąta. Złoty prostokąt jest podzielony na mniejsze kwadraty i prostokąty na podstawie Złotego Podziału, spirala narysowana w mniejszych obiektach to Złota Spirala.
Według Elliotta i jego uczniów rynek finansowy ma tę samą matematyczną podstawę, co zjawiska naturalne. Wyidealizowana lub bliska idealnej fali, fala rzeczywista jest doskonałą bazą do budowy Złotej Spirali, którą można analizować za pomocą współczynników Fibonacciego. Analizując wykres ceny rzeczywistej, nie będziemy obliczać proporcji i konstruować obiektów Fibonacciego mierząc długości i prostokąt. Proponuję przeanalizować wykres wykorzystujący wbudowane możliwości TradingView.
Analiza proporcji
Analiza proporcji to ocena proporcjonalnej zależności, w czasie i amplitudzie, jednej fali do drugiej. Jeśli znacie moje artykuły szkoleniowe wyjaśniające podejście Billa Williamsa (Część 1 i Część 2), prawdopodobnie pamiętacie, że pisałem o związkach między długościami różnych fal.
W przeciwieństwie do Billa Williamsa, Prechter dzieli związki fal na dwie kategorie:
- związki między cofnięciami;
- związki między naprzemiennymi falami lub falami rozwijającymi się w tym samym kierunku,
Związki między cofnięciami
Korekta często odwzorowuje procent Fibonacciego poprzedniej fali. Williams przeanalizował rozmiar cofnięcia w zależności od pozycji. Na przykład, druga fala najczęściej cofa się o 38,2% –61,8% długości pierwszej fali, a czwarta fala przeważnie o 38,2–50% trzeciej fali.
Prechter odnosi się jednak do długości korekty w zależności od rodzaju cofnięcia. Na przykład, ostre korekty mają tendencję do cofnięcia o 61,8% lub 50% poprzedniej fali. Co ciekawe, Prechter zgadza się z Williamsem, że ostre korekty najczęściej występują na fali 2. Często pojawiają się one również jako podfale B większego zygzaka lub podfale X w wielokrotnym zygzaku.
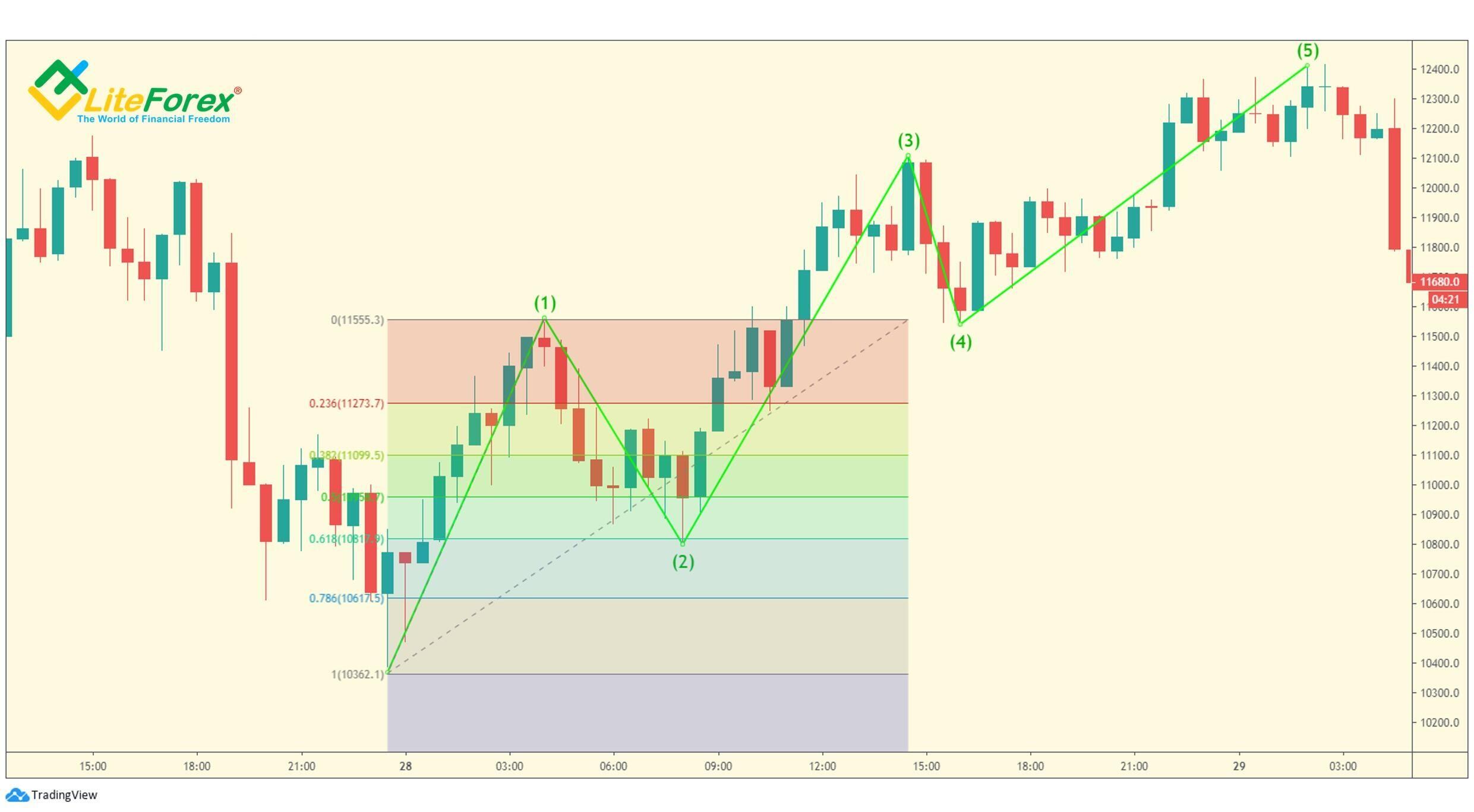
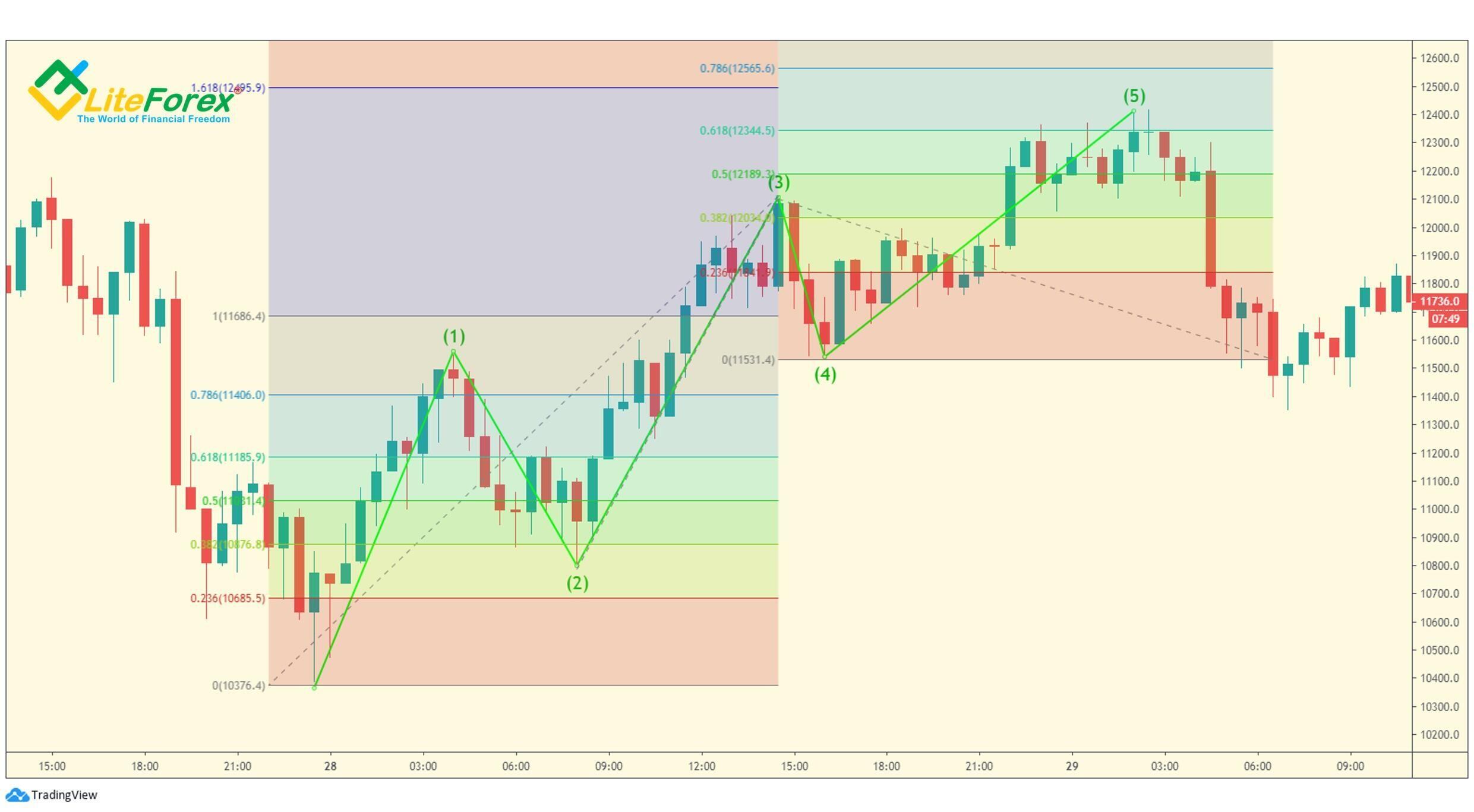
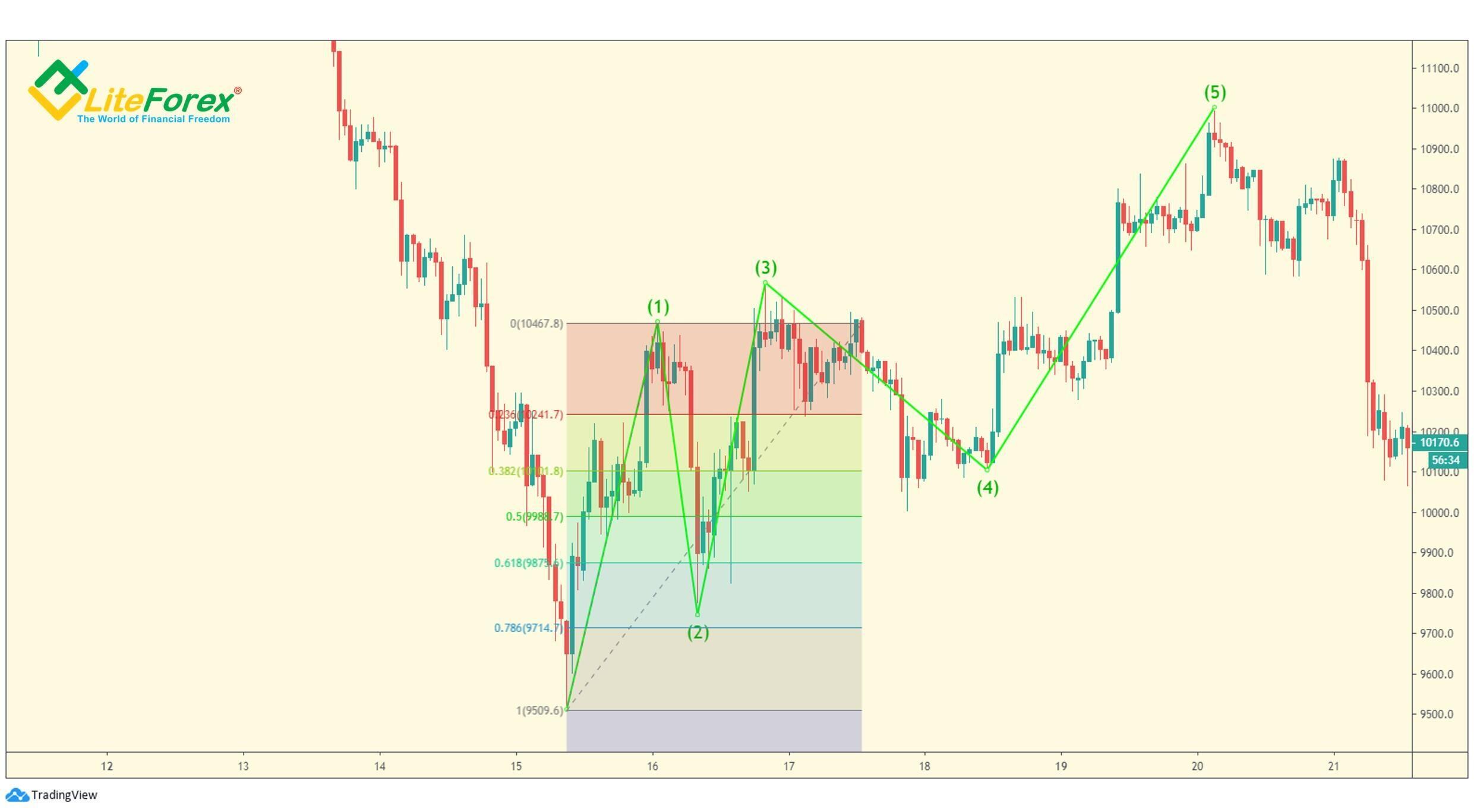
Wykres BTCUSD przedstawia przykład sekwencji pięciu fal. Fala (2) to ostra korekta. Fala ta cofa się o 61,8% fali 1 (niebieski obszar, około 10800 USD na wykresie).
Korekty boczne są z reguły znacznie mniejsze i zwykle cofają się o 38,2% poprzedniej fali impulsowej, szczególnie gdy występują jako fala 4.
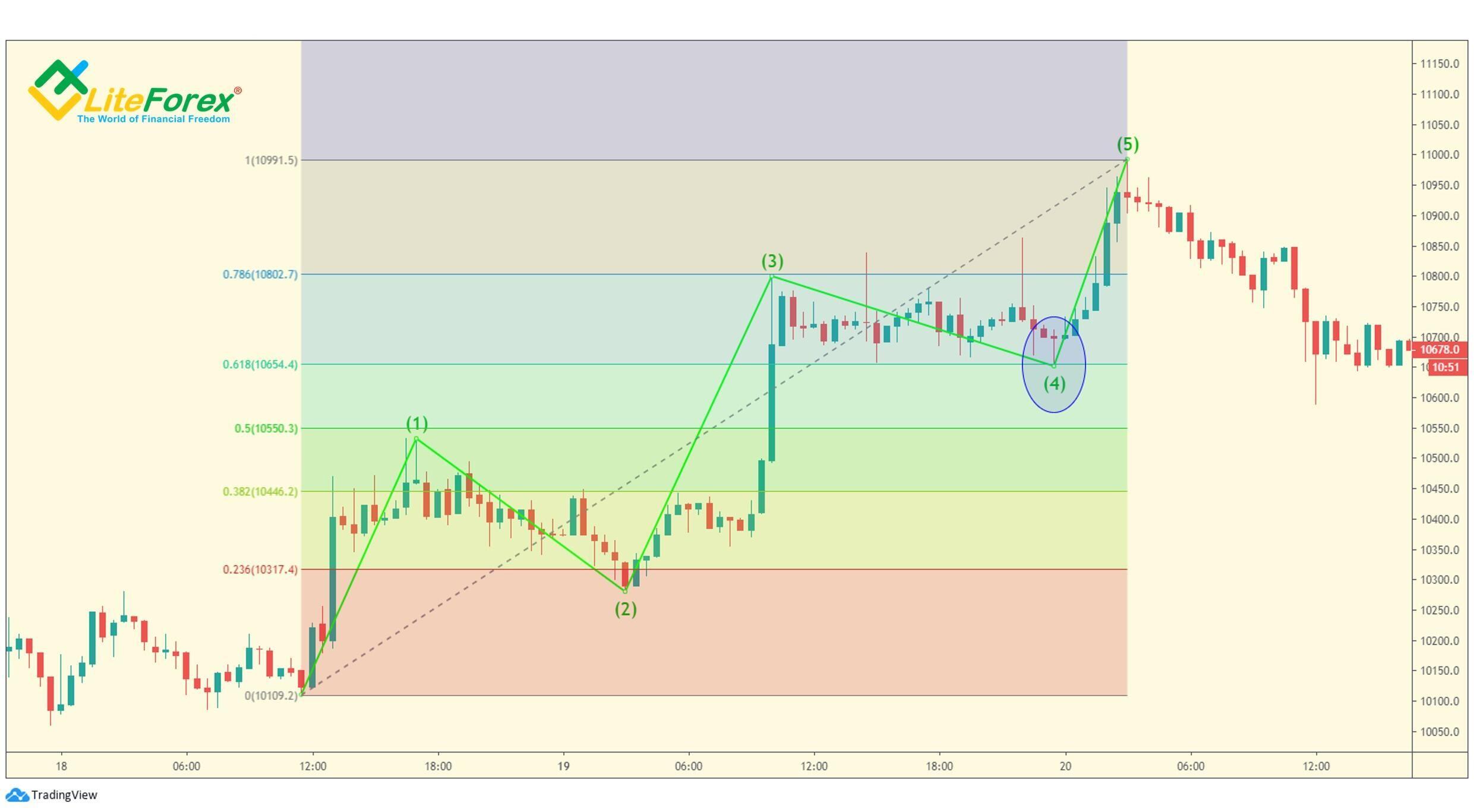
Powyższy wykres przedstawia przykład płaskiej (lub bocznej) korekty jako fali 4. Jak widać, cofnięcie w tej fali jest raczej krótkie, zawiera się między 23,6% a 38,2% trzeciej fali, na poziomie 10640 USD. Jak widać z dwóch powyższych przykładów, dokładność współczynników cofnięcia ma pewne odchylenie, ale nadal pozwala zidentyfikować przybliżone granice i kierunek ruchu. Ważne jest to, aby postrzegać te cele jako zwykłe tendencje i brać pod uwagę odchylenia od rzeczywistego ruchu.
Niemniej jednak ta metoda jest dość popularna, pomiar cofnięcia jest łatwy. O wiele bardziej precyzyjne i niezawodne są jednak proporcje między naprzemiennymi falami lub długościami rozwijającymi się w tym samym kierunku.
Wielokrotności fali motywacyjnej
W poprzednich artykułach pisałem, że gdy fala 3 się przedłuża, pozostałe fale zmierzają w kierunku równości lub związku 0,618. Zależność ta odpowiada wszystkim motywacyjnym i impulsowym falom, których długości odnoszą się do siebie zgodnie z matematycznymi założeniami Fibonacciego, w proporcjach od 1 do 1,618 lub 2,618 (przy odwróconych proporcjach 0,618 i 0,382).
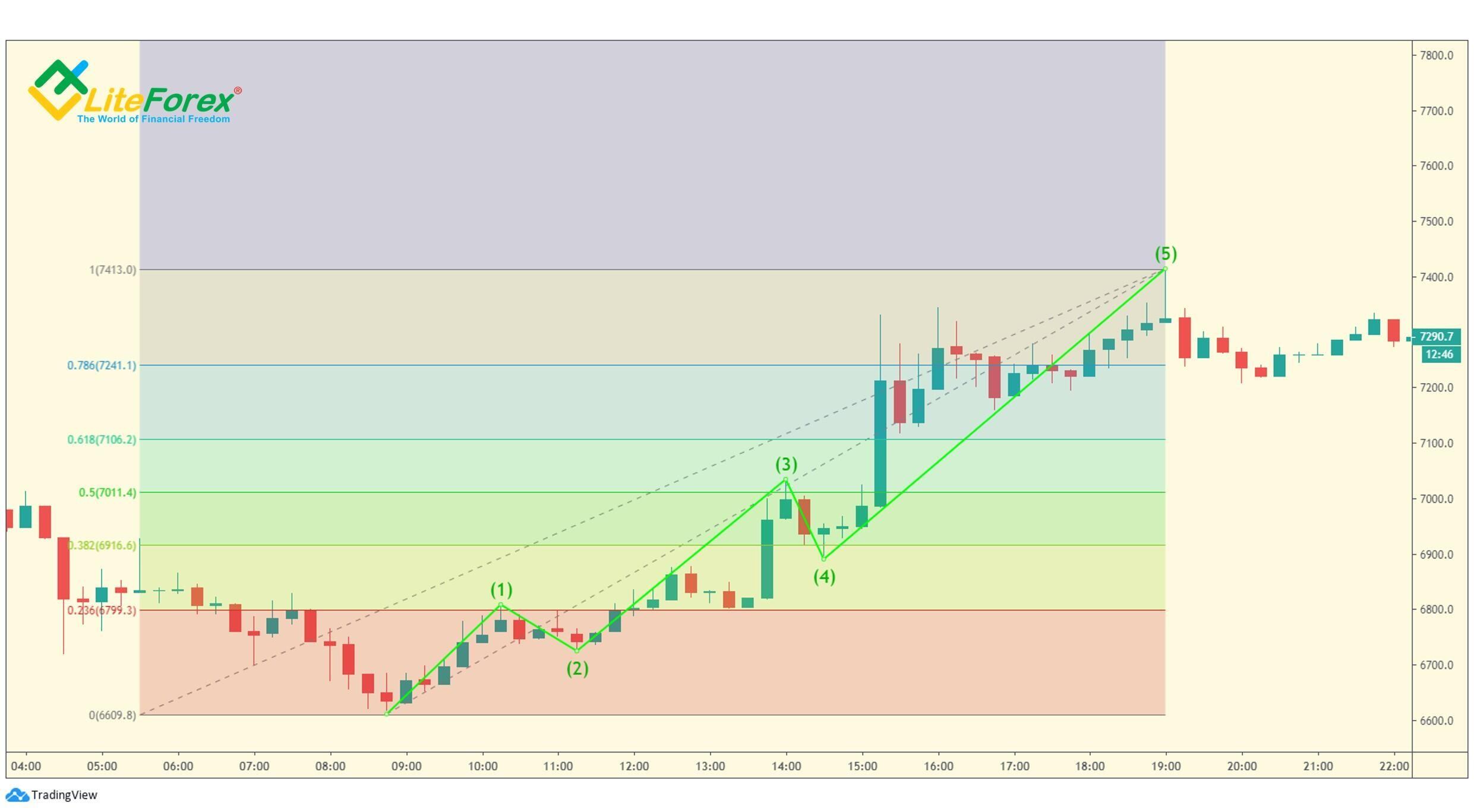
Powyższy wykres przedstawia związek między falą 1 i falą 3 w porównaniu z długością fali 3. Kolorowe obszary oznaczają poziomy Fibonacciego związane z długością fali 3. Jak widać, fala 1 jest mniej więcej równa fali 3, a stosunek fali 5 wynosi 0,618.
Pierwsza fala nie jest przedłużeniem, ale czwarta prawdopodobnie podzieli zakres cenowy zgodnie ze Złotym Podziałem. Oznacza to, że odległość od początku pierwszej fali do punktu końcowego fali 4 wynosi 61,8% całego impulsu, a fali 5 - 38,2%.
Na powyższym przykładzie mamy do czynienia z formacją regularnych fal motywacyjnych. Fala 4 kończy się dokładnie na turkusowej linii z wartością 0,618.
W przypadku rozszerzonej piątej fali stosunek jest odwrotny. Odległość między początkiem pierwszej fali a szczytem fali 4 wynosi 38,2% całego impulsu, a fali piątej 61,8%.
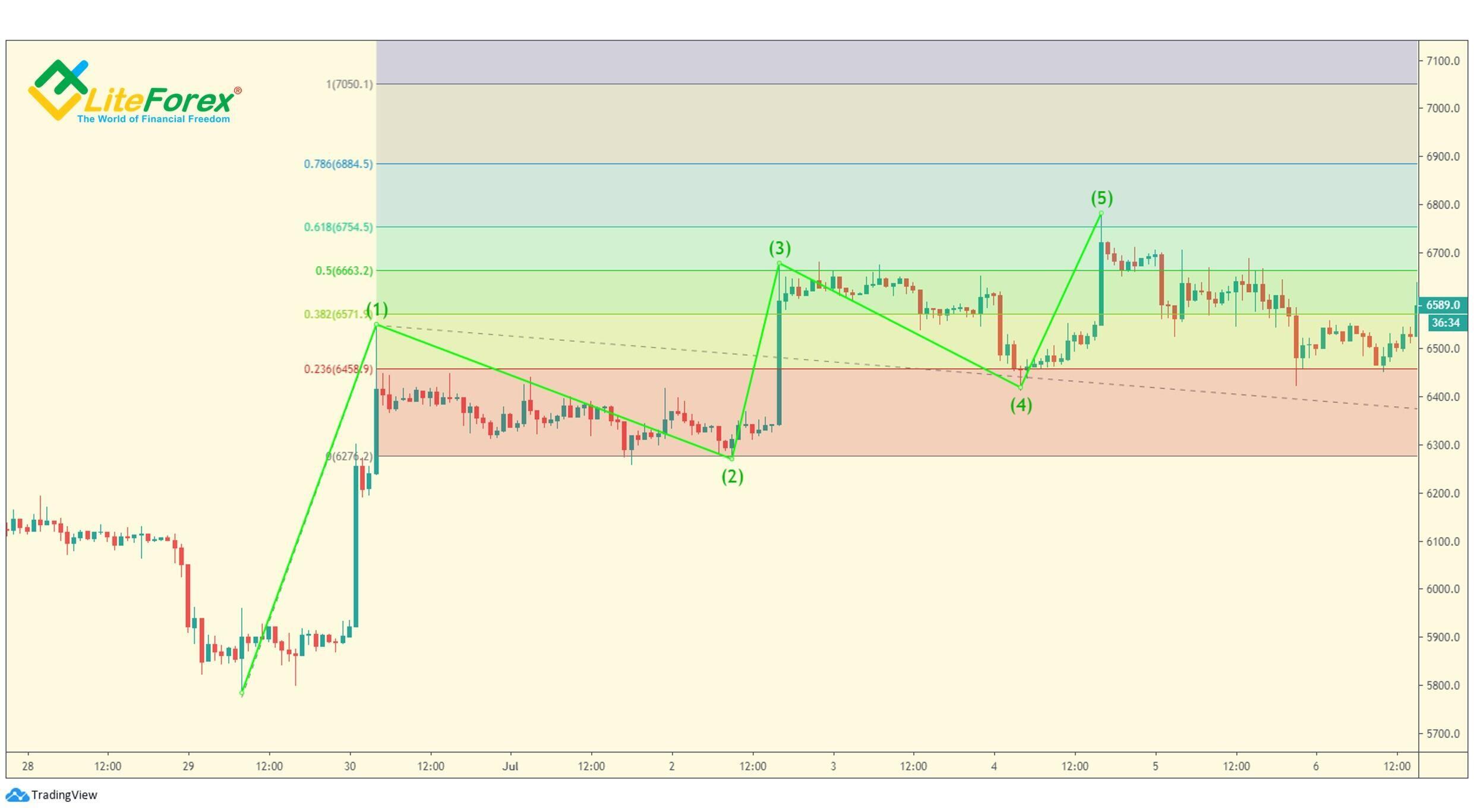
15-minutowy wykres BTCUSD przedstawia pięciofalowy wzór z wydłużoną piątą falą. Szczyt fali 4 znajduje się w żółtym obszarze, więc długość fal 1, 2, 3, 4 to nieco mniej niż 38,2% całej formacji falowej. W związku z tym piąta fala stanowi 61,8% całego pięciofalowego wzoru.
Dlatego wytyczne te są dość swobodnie interpretowane w odniesieniu do punktu w ramach czwartej fali, którym jest Złoty Podział impulsu pięciofalowego. Może to być początek, koniec i punkt zakończenia cofnięcia. Tak więc w procesie przewidywania punktu końcowego fali 5 za pomocą analizy współczynnika można zdefiniować przybliżony obszar szczytu, który składa się z kilku punktów docelowych znajdujących się obok siebie.
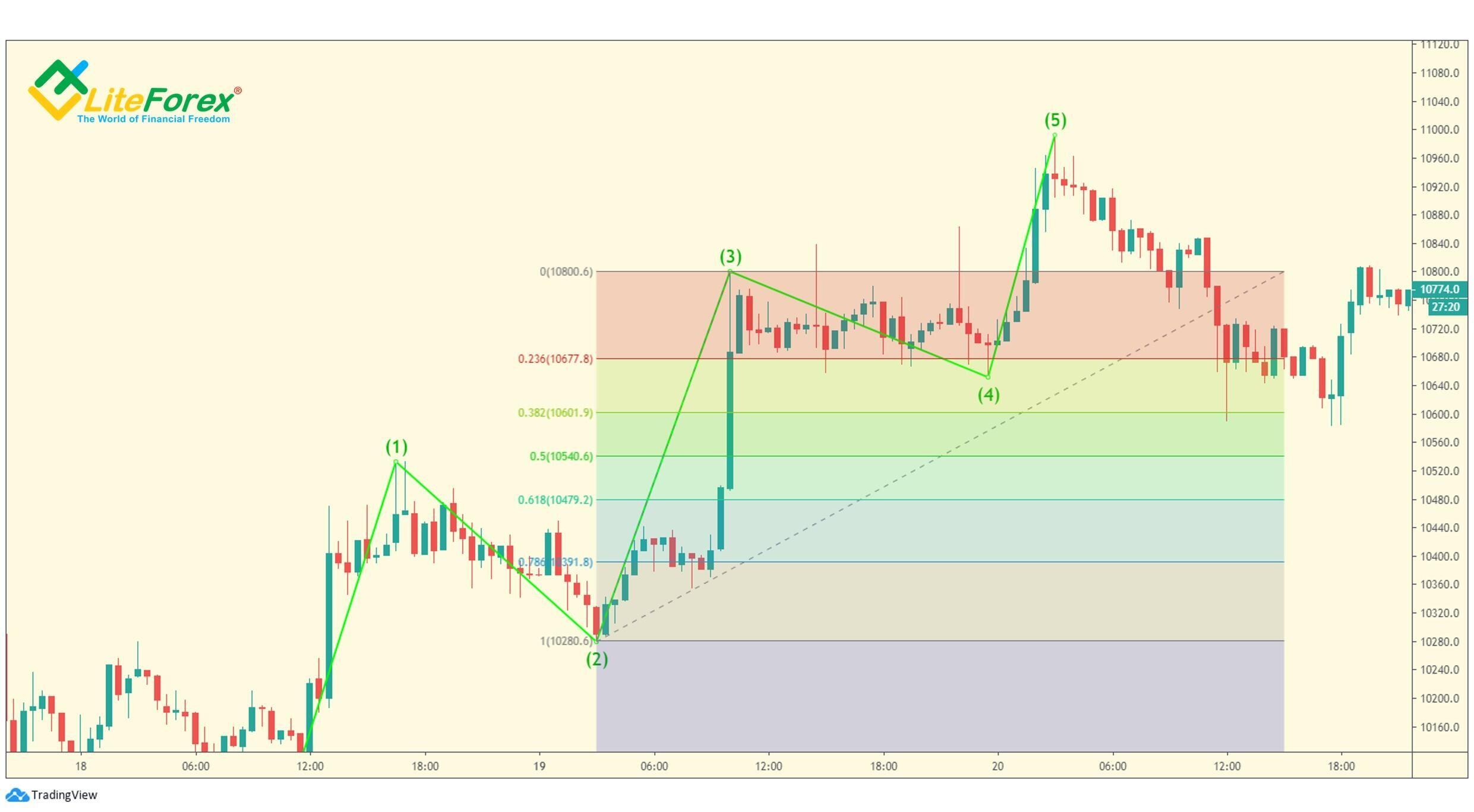
W tych rzadkich przypadkach, gdy fala 1 jest przedłużona, fala 3 i fala 5 będą równe 0,382 lub 0,618 fali 1, gdy zaczniecie liczyć od punktu zakończenia drugiej fali.
Powyższy wykres cenowy BTCUSD przedstawia pięciofalową sekwencję, której pierwsza fala jest przedłużona. Następnie rzut (1) jest dołączony do punktu początkowego fali trzeciej. Kolorowe obszary oznaczają poziomy Fibonacciego. Widać, że długości fal (3) i (5) to około 61,8% fali (1), co potwierdza powyższe założenie.
Wielokrotności fali korekcyjnej
W zygzaku długość fali C jest zwykle równa długości fali A. Jednak proporcje 1,618 lub 0,618 również nie są rzadkie.
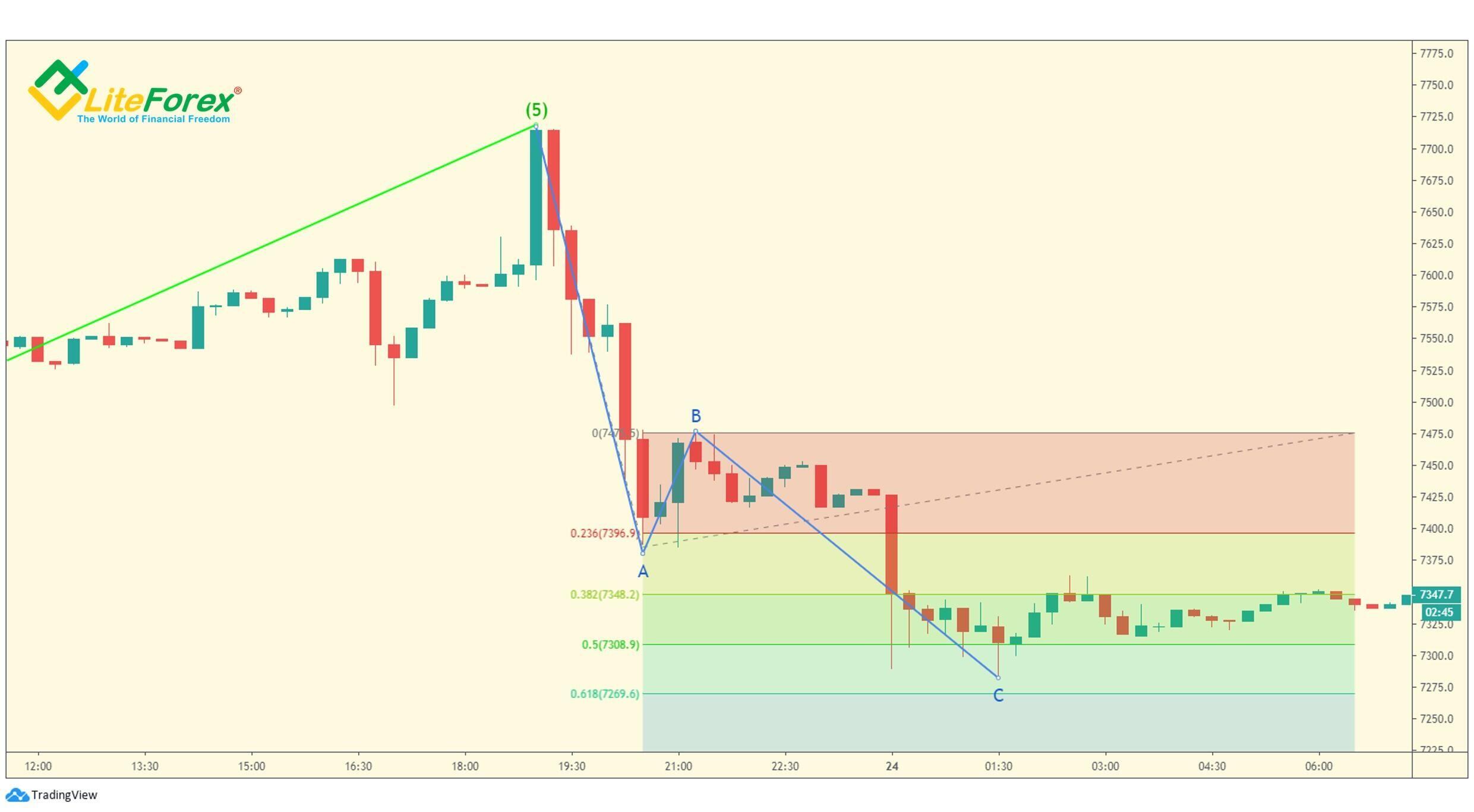
Powyższy wykres przedstawia regularny zygzak. Fala C wzoru korekcyjnego sięga prawie 61,8% projekcji fali A.
Ten sam stosunek jest wykorzystywany w przypadku złożonych zygzaków, w których porównuje się proste tworzące je zygzaki.
Przykład wielokrotnego (złożonego) zygzaka przedstawiono powyżej. Dokładniej, jest to podwójny zygzak, w którym długość zygzaka (W) jest w przybliżeniu równa długości zygzaka (Y). Jak widać na wykresie, koniec drugiego zygzaka jest nieco wyższy niż rzut pierwszego i wpada on do niebieskiej strefy, która zaczyna się powyżej 100% długości pierwszego zygzaka.
Jak pamiętacie z poprzednich artykułów szkoleniowych, fale w regularnej płaskiej korekcie są w przybliżeniu równe. W rozszerzonej korekcie płaskiej fala C jest często 1,618 razy większa od długości fali A.
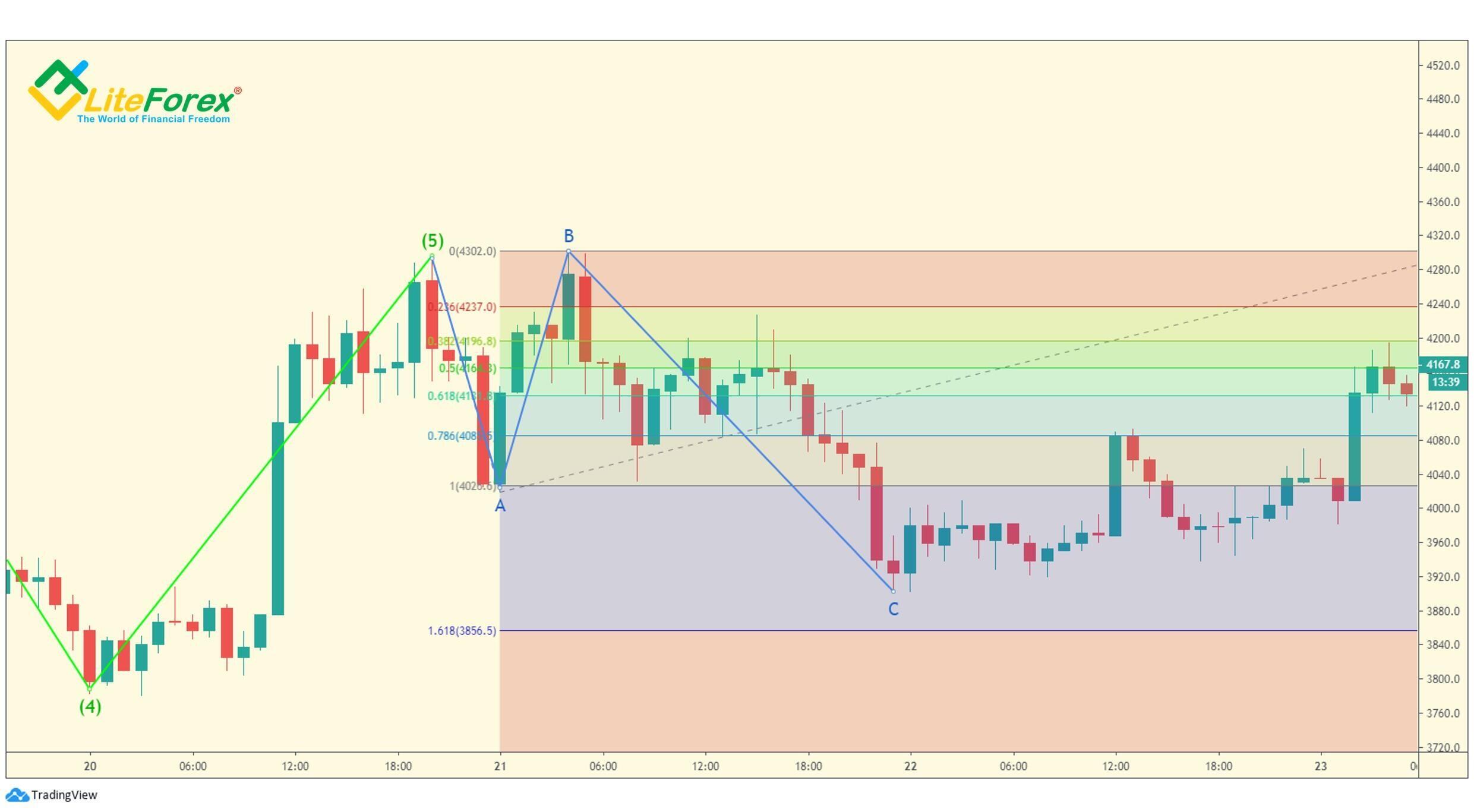
Powyższy wykres przedstawia rozszerzoną płaską korektę. Fala C w formacji kończy się w niebieskim obszarze i nie osiąga cofnięcia wynoszącego 1,618. Może tak się zdarzyć, ponieważ fala B znajduje się nieco powyżej punktu końcowego piątej fali impulsowej, a zatem kolejne cofnięcie nie jest wystarczająco wspierane przez niedźwiedzie.
Fala B w rozszerzonym flacie czasami jest o 1,236 lub 1,382 razy dłuższa niż fala A. Jednak, jak pokazuje powyższy przykład, w rzadkich przypadkach mogą istnieć wyjątki.
W trójkątach co najmniej dwie z fal naprzemiennych są zwykle powiązane ze sobą proporcją wynoszącą 0,618. W zwężającym się trójkącie można spotkać następujące proporcje:
- Fala E to 0,618 fali C;
- Fala C 0.618 to fali A;
- Fala D 0.618 to fali B.
Wykres przedstawia wielokrotną korektę, która składa się z trójkąta i rozszerzonego flata. Kolorowe obszary oznaczają stosunek długości do fali A przy pomocy wielokrotności od 0 do 4,236. Jak widać, fala C ma zasięg równy 61,8% fali A.
W rozszerzonych formacjach wielokrotność wynosi 1,618. W rzadkich przypadkach sąsiednie fale są powiązane przez te współczynniki.
W złożonych korektach ruch jednego prostego wzoru jest czasami powiązany proporcjami równymi lub wynoszącymi 0,618. W rzadkich przypadkach możliwe są inne relacje. Prawdopodobieństwo takiego zdarzenia wzrasta, jeśli jednym z prostych modeli jest trójkąt.
Wielokrotne relacje falowe
Opisane powyżej relacje można wykorzystać na dwa sposoby. Po pierwsze, w procesie powstawania struktur falowych, narzędzie to pomaga potwierdzić poprawność interpretacji sekwencji powstawania fal i aktualnych pozycji. Po drugie, relacje te można wykorzystać do prognozowania przyszłych ruchów cenowych, ponieważ jeśli trend odwróci się na jednym z poziomów Fibonacciego, będzie to punkt dwa razy bardziej znaczący.
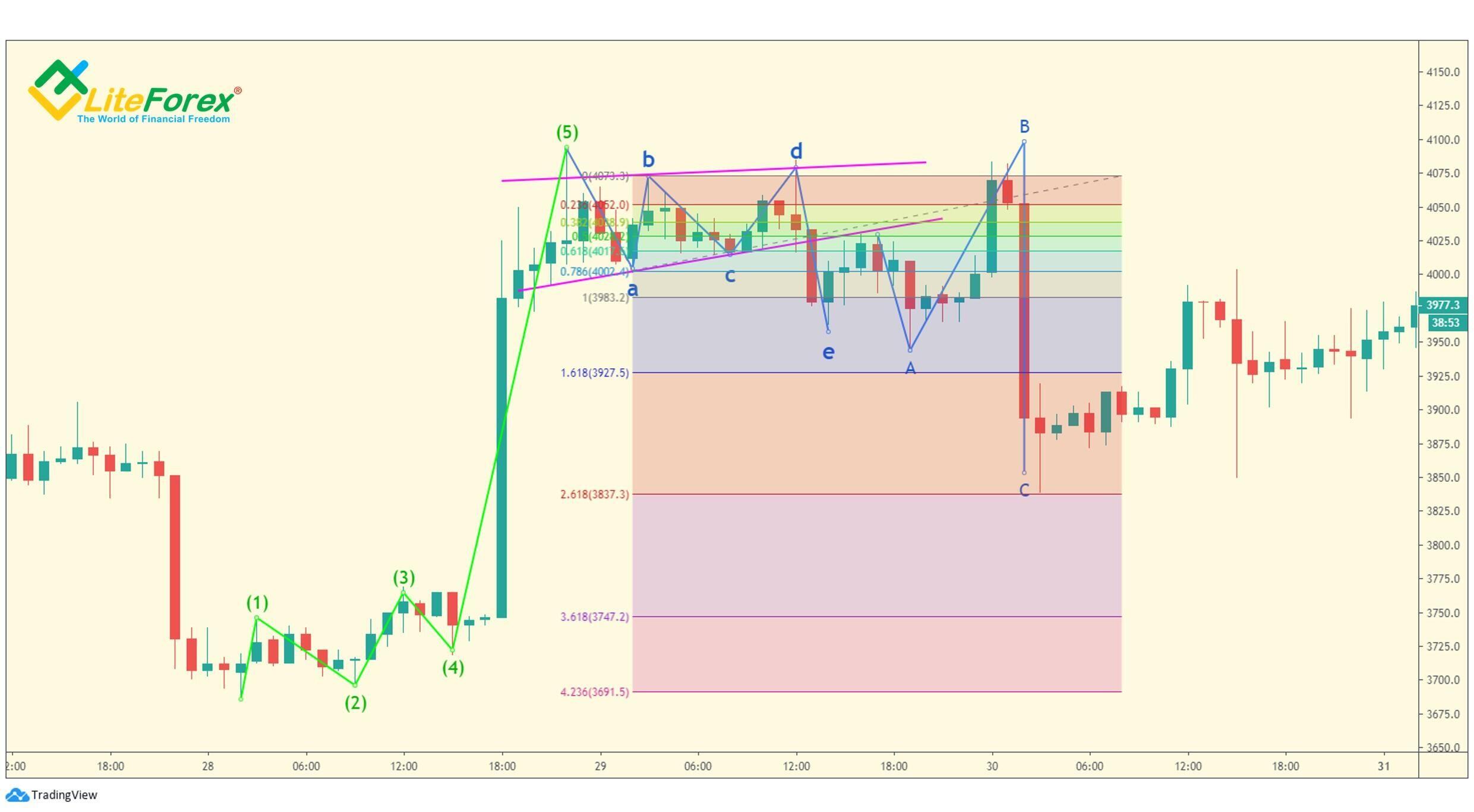
Ważne jest to, że prognozy oparte na wielu proporcjach Fibonacciego są zwykle dokładniejsze. Na przykład, w oparciu o wyjaśnione powyżej relacje między falą 1, falą 5 i falą 3, która jest przedłużona (od 1 do 0,382 lub 0,618), można przewidzieć prawdopodobny punkt zakończenia fali 5. Inny prawdopodobny punkt można określić obliczając długość całej formacji na podstawie zasięgu pierwszych czterech fal, co powinno stanowić 61,8% całej długości. Przeanalizujmy ten przykład.
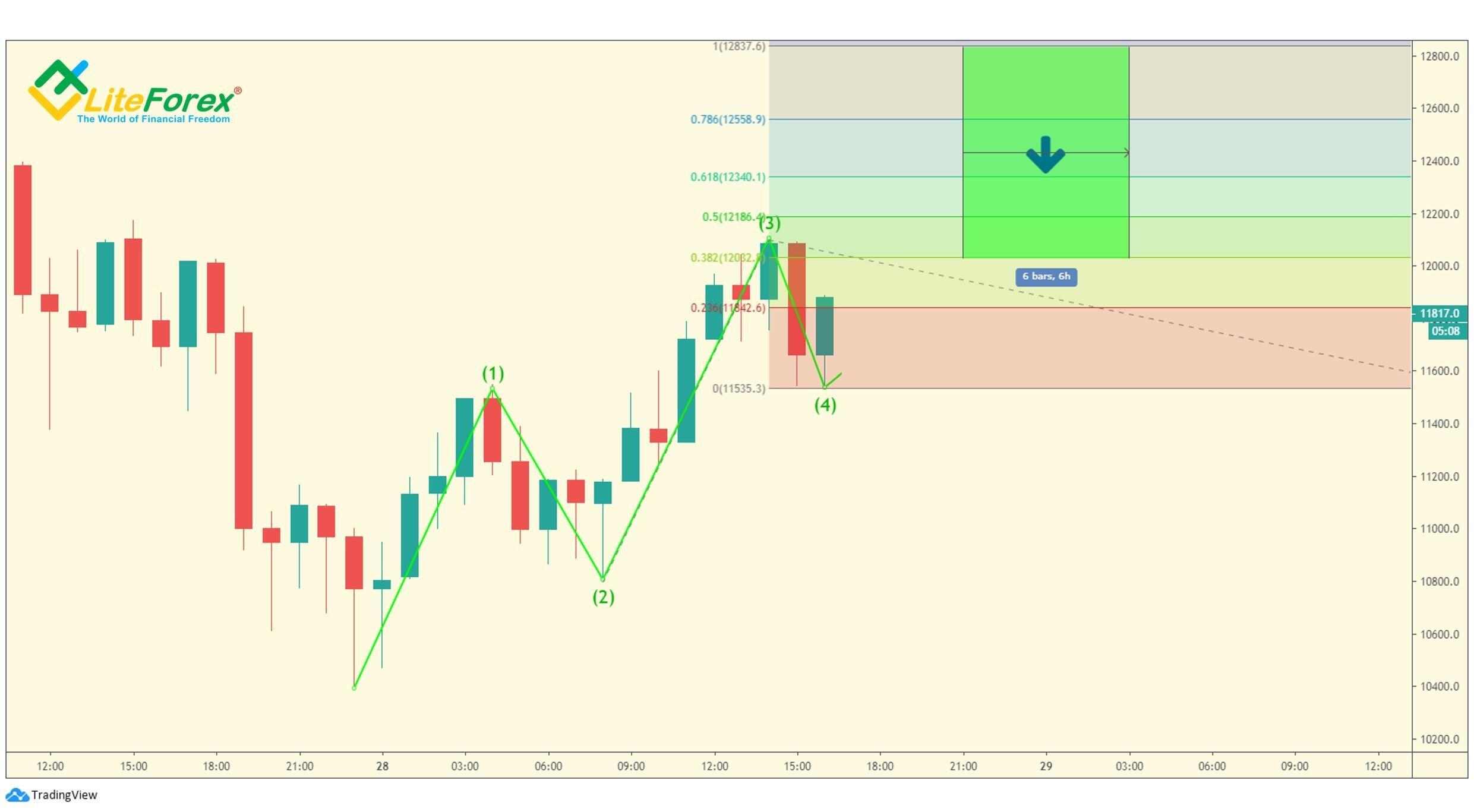
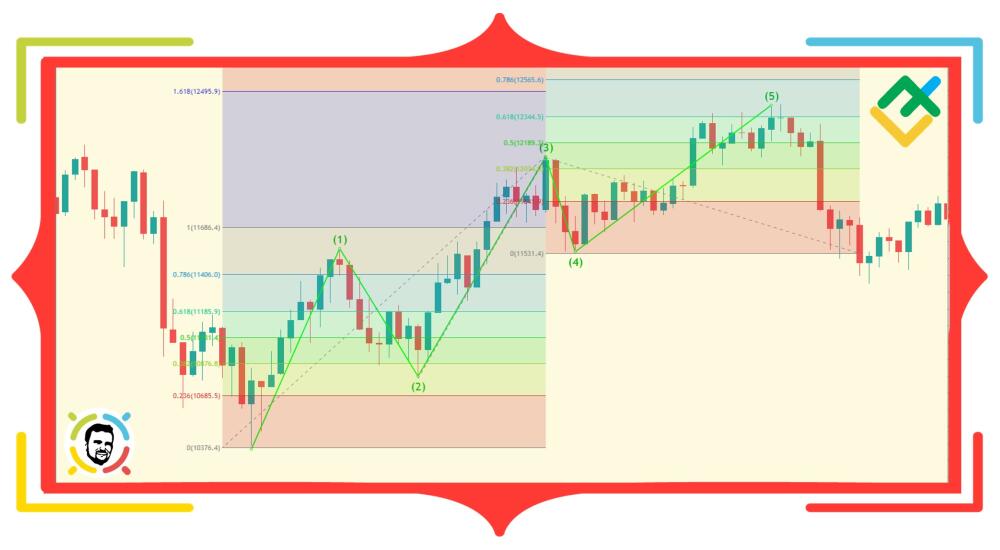
Gdy fala trzecia się wydłuża, możemy założyć, że fala piąta będzie wynosiła od 38,2% do 100% jej zasięgu (jest zaznaczona jasnozielonym obszarem na wykresie). Najbardziej prawdopodobny stosunek to 61,8% zakresu fali 3 (zaznaczony niebieską strzałką).
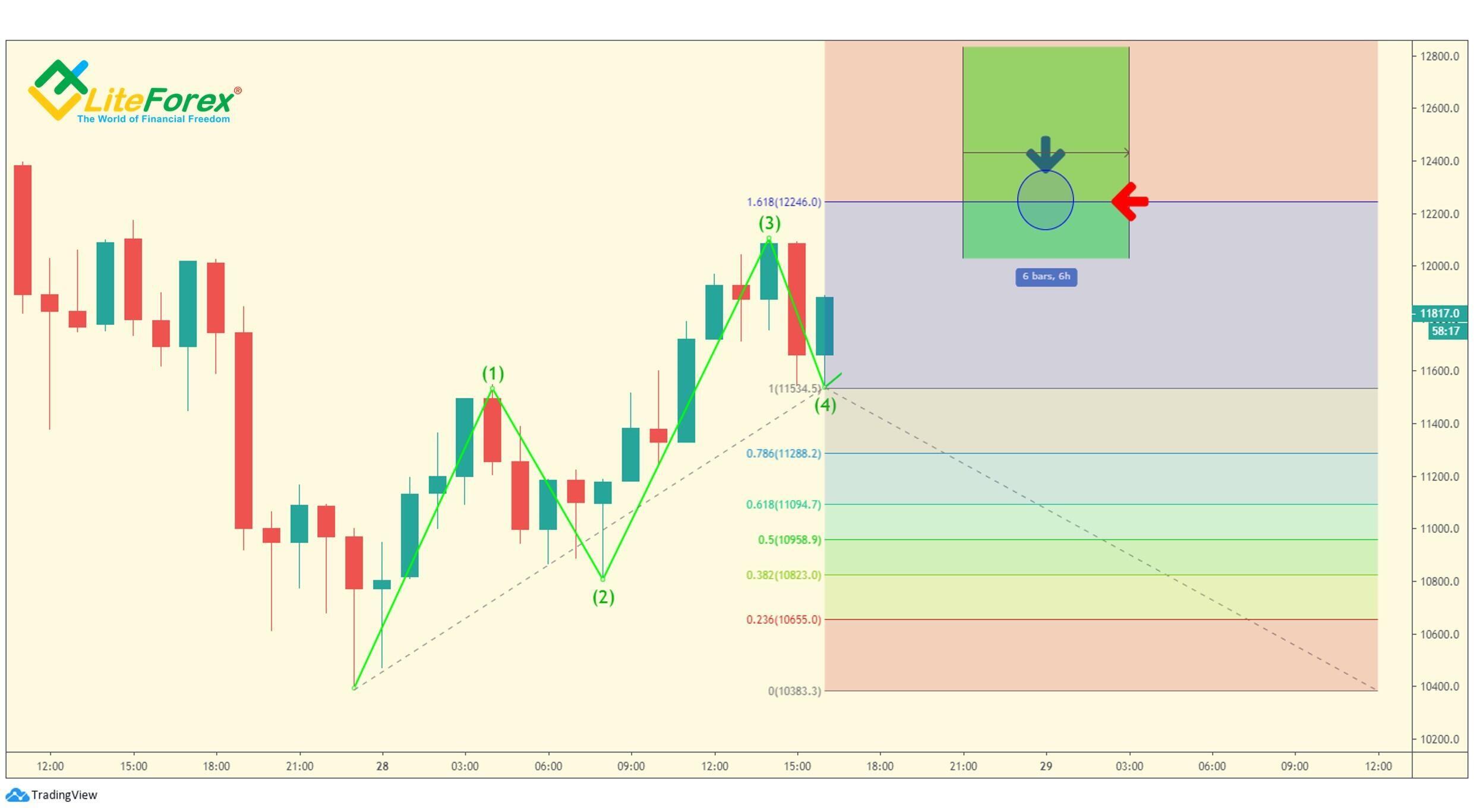
Zostawmy zakładany obszar zakończenia fali 5 na wykresie i znajdźmy nasz ogólny zakres całej pięciofalowej sekwencji. Załóżmy, że początek fali 1 to 0, a koniec fali 4 to 1, możemy określić prawdopodobny poziom punktu zakończenia formacji na 1,618 (czerwona strzałka na wykresie). Następnie dopasowujemy prawdopodobny punkt odwrócenia widoczny w poprzednich obliczeniach i możemy teraz wyznaczyć dość wąski zakres (niebieskie kółko). Odwrócenie może nastąpić w tym obszarze, zwłaszcza jeśli pojawiają się sygnały zakończenia trendu i gdy cena zbliża się do poziomu oporu.
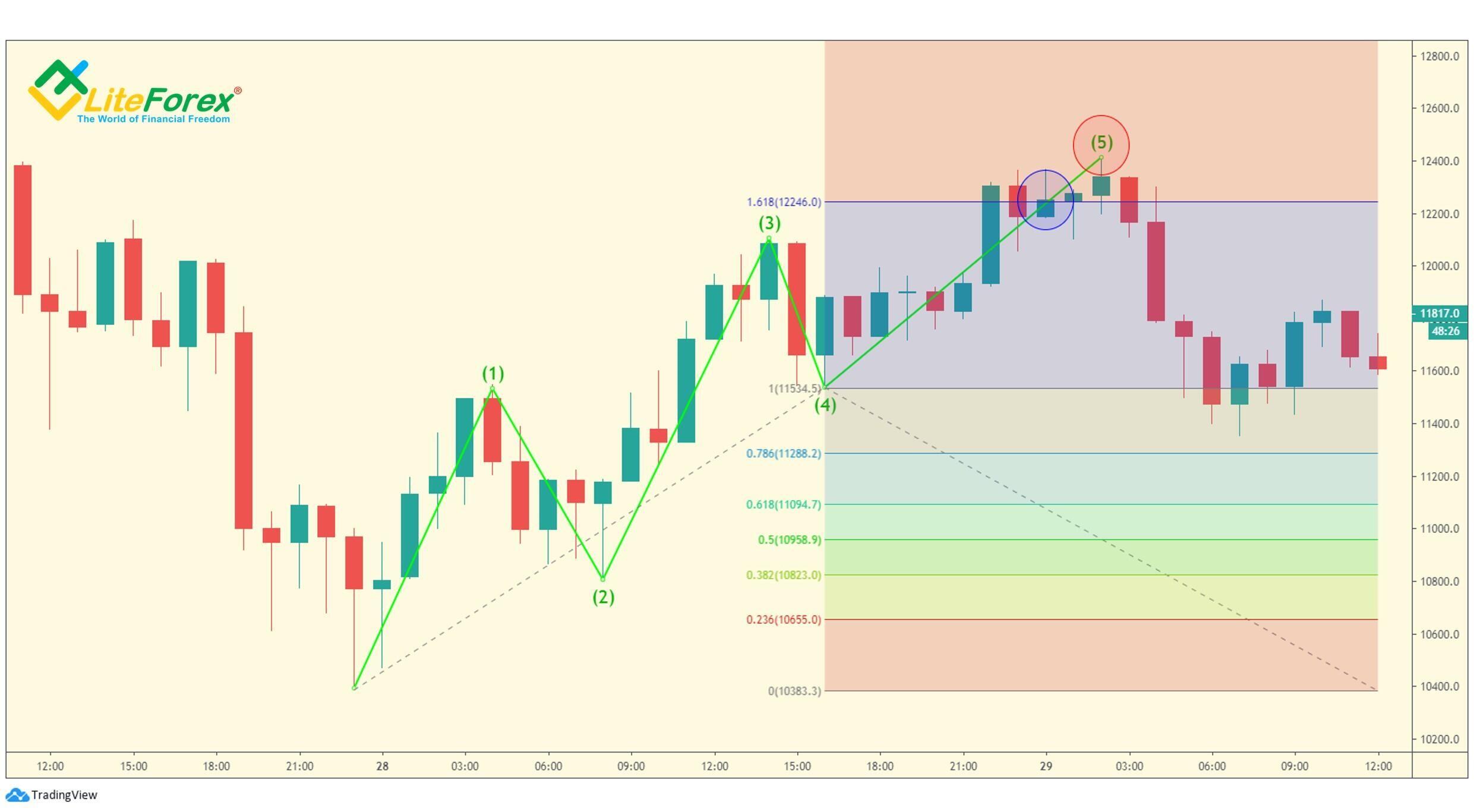
Jak widać, trend zmienia się nieco powyżej założonego zakresu. To całkiem niezły wynik, biorąc pod uwagę to, że został określony na podstawie samej analizy proporcji. Poza tym, zanim cena zbliżyła się do sugerowanego punktu Pivota, mogliśmy stwierdzić, że piąta fala również ma złożoną strukturę i charakteryzuje się ostrymi skokami cenowymi. A zatem przejście nieco wyżej niż poziom oporu jest całkiem normalnym zjawiskiem.
Pragnę zaznaczyć, że w handlu dziennym nie polecam podejmowania decyzji handlowych wyłącznie w oparciu o analizę proporcji, ponieważ zawiera ona szeroki zakres możliwości i nie może dać jasnej wskazówki, gdzie dokładnie trend się zmieni. Lepiej stosować analizę proporcji razem z innymi narzędziami analitycznymi. Co więcej, te ostatnie należy traktować jako sygnały podstawowe, a poziomy Fibonacciego jako potwierdzenie oporu na założonym poziomie.
Co się stanie, jeśli współczynniki się nie sprawdzą?
W handlu praktycznym można wielokrotnie spotkać się z przypadkami, gdy rynek ignoruje poziomy Fibonacciego. Czy powinniście być rozczarowani, jeśli cena przebije jeden z przewidywanych poziomów? Wręcz przeciwnie, takie wydarzenie dostarcza dodatkowe i cenne informacje.
Przełamanie sugeruje, że odwrócenie może nastąpić na następnym poziomie. I jest to najczęściej dość duża odległość, która może generować dodatkowy zysk. Z drugiej strony, jeśli wyznaczone punkty nie zostaną osiągnięte lub znajdują się za daleko, jest to powód do zrewidowania waszej interpretacji dotyczącej powstawania fali. W prawdziwym handlu fale rzadko mają wyidealizowane struktury. Traderzy z reguły mają kilka wersji bieżącej interpretacji trendów i trzymają się jednej z nich, dopóki nie zadziała lub zostanie anulowana, wtedy korzystają z innej wersji.
Powyższy wykres przedstawia nieregularną sekwencję falową. Ma ona zbyt ostre cofnięcia. Na przykład fala druga z łatwością przebija poziom 0.618. Jeśli nie ma innych sygnałów Pivota, nie powinno was to zmylić. Nowym poziomem wsparcia w tym przypadku jest poziom 0,786. Jak widać, trend się odwrócił, zanim cena osiągnęła ten poziom. Nie należy jednak zapominać, że druga fala musi znajdować się wyżej w punkcie zakończenia niż początek pierwszej fali. Jeśli cena znowu spadła przebijając poziom 0,786, powinniśmy zrewidować interpretację sytuacji rynkowej.
Na tym chciałbym zakończyć cykl artykułów szkoleniowych poświęconych zasadzie fali rynkowej opracowanej przez Roberta Prechtera. Po przestudiowaniu tego obszaru teorii fal Elliota, a także podejścia opracowanego przez Billa Williamsa, możemy wyodrębnić najbardziej efektywne narzędzia z obu podejść i zbudować własną strategię handlu kryptowalutami w oparciu o teorię fal Elliota. I właśnie to zrobimy następnym razem.
Życzę powodzenia i dużych zysków!
P.S. Podobał się mój artykuł? Udostępnij go w sieciach społecznościowych, najlepszy sposób na podziękowanie:)
Wykres cen BTCUSD w czasie rzeczywistym
Treść tego artykułu stanowi wyłącznie prywatną opinię autora i może nie pokrywać się z oficjalnym stanowiskiem LiteForex. Materiały publikowane na tej stronie mają wyłącznie charakter informacyjny i nie mogą być traktowane jako porada inwestycyjna ani konsultacja w rozumieniu dyrektywy 2014/65/UE.
Zgodnie z przepisami prawa autorskiego artykuł ten jest chronionym obiektem własności intelektualnej, co obejmuje zakaz kopiowania i rozpowszechniania bez zgody.