Drodzy przyjaciele!
W poprzednim artykule opisałem flaty i zygzaki, ich odmiany oraz zasady powstawania. Jeśli nie czytaliście poprzednich artykułów z serii NeoWave, polecam przeczytanie wszystkich artykułów poświęconych teorii NeoWave opracowanej przez Glenna Neely’ego w książce Mastering Elliott Wave, zaczynając od pierwszego.
Teoria Neo Wave. Część 1. Zasady tworzenia wykresów
Teoria Neo Wave. Część 2. Podstawowe informacje dotyczące Polifal i Etykiet Struktur
NeoWave. Część 3. Zasada zniesienia 1.
Teoria NeoWave. Część 4. Zasada zniesienia 2.
Teoria NeoWave. Część 5. Zasada zniesienia 3.
NeoWave. Część 6. Zasada zniesienia 4. Warunki “a” i “b”
NeoWave. Część 7. Zasada zniesienia 4. Warunki “c”, “d” i “e”
NeoWave. Część 8. Zasada zniesienia 5. Warunki “a” i “b”
NeoWave. Część 9. Zasada zniesienia 5. Zasada zniesienia 6, warunek “a”.
NeoWave. Część 10. Zasada zniesienia 6. Warunki “b”, “c” i “d”
NeoWave. Część 11. Zasada zniesienia 7.
NeoWave. Część 12. Impulsy i zasady analizowania impulsowych wzorów fal
NeoWave. Część 13. Korekty. Zasady identyfikowania korekty.
W tym artykule opiszę najbardziej złożone wzory fal Elliotta, trójkąty. Opiszę odmiany trójkątów oraz kryteria niezbędne do identyfikacji wzorów trójkątów, oczywiście zgodnie z teorią NeoWave.
Artykuł obejmuje następujące tematy:
Wzory trójkątów w fali Elliotta
Niektóre z najtrudniejszych wzorów korekcyjnych to odmiany trójkątów. Nie mają określonych ograniczeń czasowych dotyczących zakończenia wzoru. Neely nie zidentyfikował również żadnej zasady dotyczącej absolutnej pewności co do kierunku akcji rynkowych po trójkątach. Poza tym trójkąty to jedne z najpopularniejszych wzorów Elliotta; dlatego ich dokładne zrozumienie jest niezbędne. Nauka rozpoznawania trójkątów na wczesnym etapie ich tworzenia może dostarczyć dokładne informacje o aktualnej sytuacji rynkowej.
Wszystkie odmiany Trójkątów spełniają poniższe minimalne wymagania:
W każdym trójkącie jest pięć segmentów. W kolejności występowania każdy segment trójkąta jest oznaczony literami a, b, c, d oraz e.
Każdy segment trójkąta reprezentuje pełną fazę korekcyjną lub trójkę („:3”). Tak więc trójkąt ma strukturę 3-3-3-3-3.
W przeciwieństwie do wzoru impulsowego, który ma tendencję do wzrostu lub spadku, wszystkie pięć segmentów trójkąta będzie oscylować nieustannie w tym samym obszarze cenowym (nakładać się) z nieznacznie rozszerzającym się lub kurczącym nastawieniem.
Trójkąt może przesuwać się nieznacznie w górę lub w dół bez wpływu na ogólne wytyczne.
Długość fali B musi zawierać się w przedziale 38,2% -261,8% fali A.
Z pięciu segmentów trójkąta cztery znoszą poprzedni segment. Znoszące segmenty są falami b, c, d oraz e. Z tych czterech segmentów, trzy muszą znieść co najmniej 50% poprzedniej fali. W rzadkim przypadku bieżącego trójkąta ten parametr może nie być całkowicie spełniony.
Tylko cztery punkty końcowe (tego samego stopnia) w trójkącie powinny znajdować się między kurczącymi się liniami trendu. Pamiętajcie, że każdy punkt końcowy reprezentuje możliwy punkt styku, który możecie wykorzystać do narysowania zbieżnych lub rozbieżnych linii trendu. Nieograniczające trójkąty zwykle są zgodne z tą zasadą, ale zdarzają się wyjątki, które mogą utworzyć piąty punkt styku.
Linia kanału przecinająca punkty końcowe fal b i d w trójkącie nazywana jest linią bazową. W teorii NeoWave jej funkcja jest podobna do linii trendu 2-4 w fali impulsowej. Dlatego istnieje ogólna zasada, że linia trendu b-d nie powinna być przerwana przez żadną część fali c lub e w trójkącie.
Kurczące się trójkąty
Kurczące się trójkąty są zdecydowanie najpowszechniejszym rodzajem trójkątów. Poniżej znajduje się lista niezbędnych elementów tworzących kurczący się trójkąt (są to minimalne wymagania dla wszystkich kurczących się trójkątów):
Po zakończeniu kurczącego się trójkąta następuje „pchnięcie”, które musi wynosić co najmniej 75% najszerszego segmentu trójkąta, a w „normalnych” warunkach nie powinno przekraczać 125% najszerszego segmentu. Poza tym najszerszy odcinek nie zawsze jest falą A. Może być falą B, a w rzadkich przypadkach falą C trójkąta.
W kurczącym się trójkącie pchnięcie musi przekraczać najwyższą lub najniższą cenę (w zależności od kierunku pchnięcia) osiągniętą podczas powstawania trójkąta. Aby uprościć analizę, Neely zaleca narysowanie dwóch równoległych poziomych linii. Jedną należy poprowadzić przez najwyższy poziom cenowy osiągnięty podczas formowania się trójkąta, a drugą przez najniższy poziom cenowy. Gdy trójkąt się rozwija, linie te pomogą przewidzieć, czego można spodziewać się po zakończeniu trójkąta. Jedynym wyjątkiem od tej reguły będzie sytuacja, gdy trójkąt wyraźnie zmierza w kierunku przeciwnym do pchnięcia.
Ostatnia fala w trójkącie nie może być najmniejszą falą pod względem czasu.
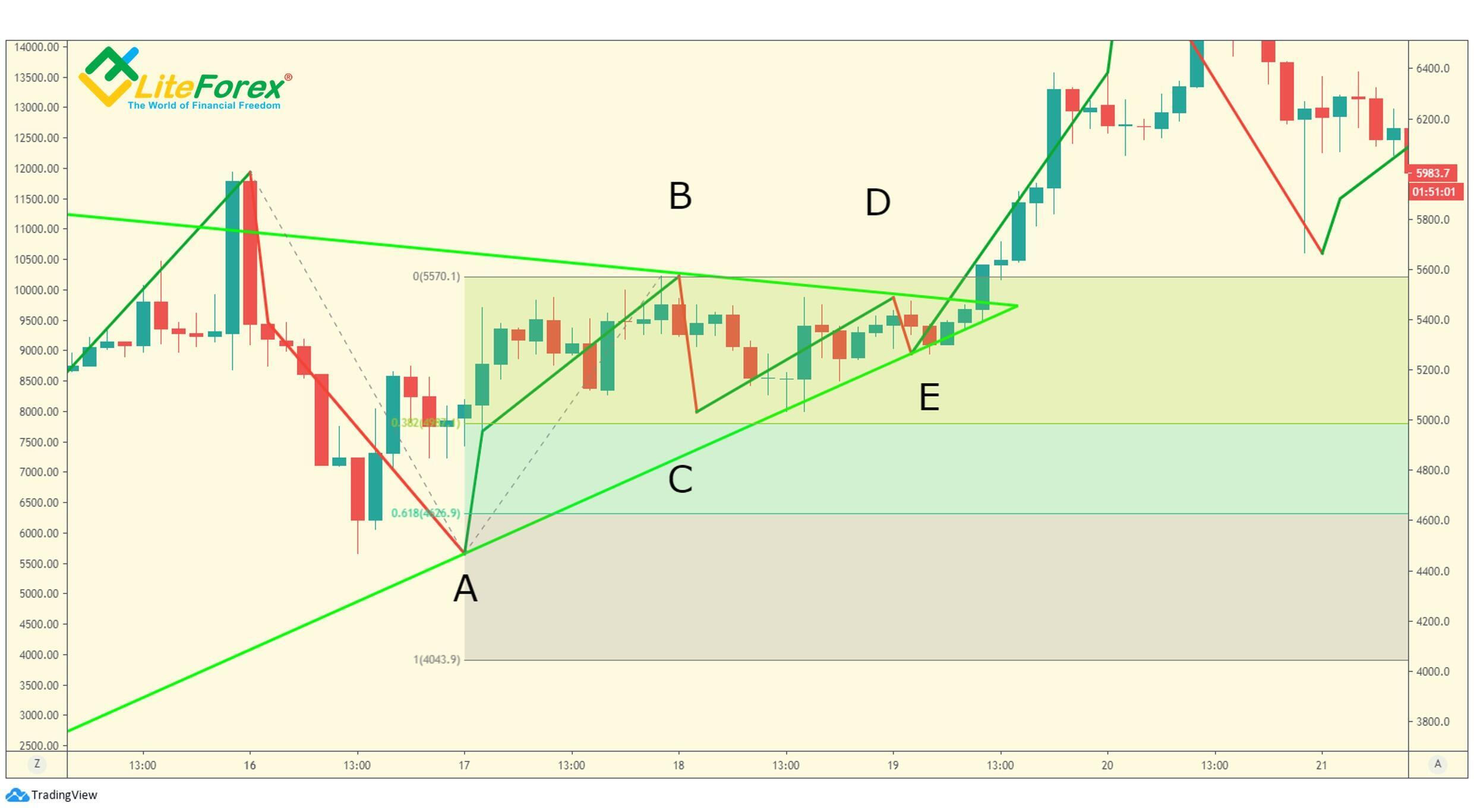
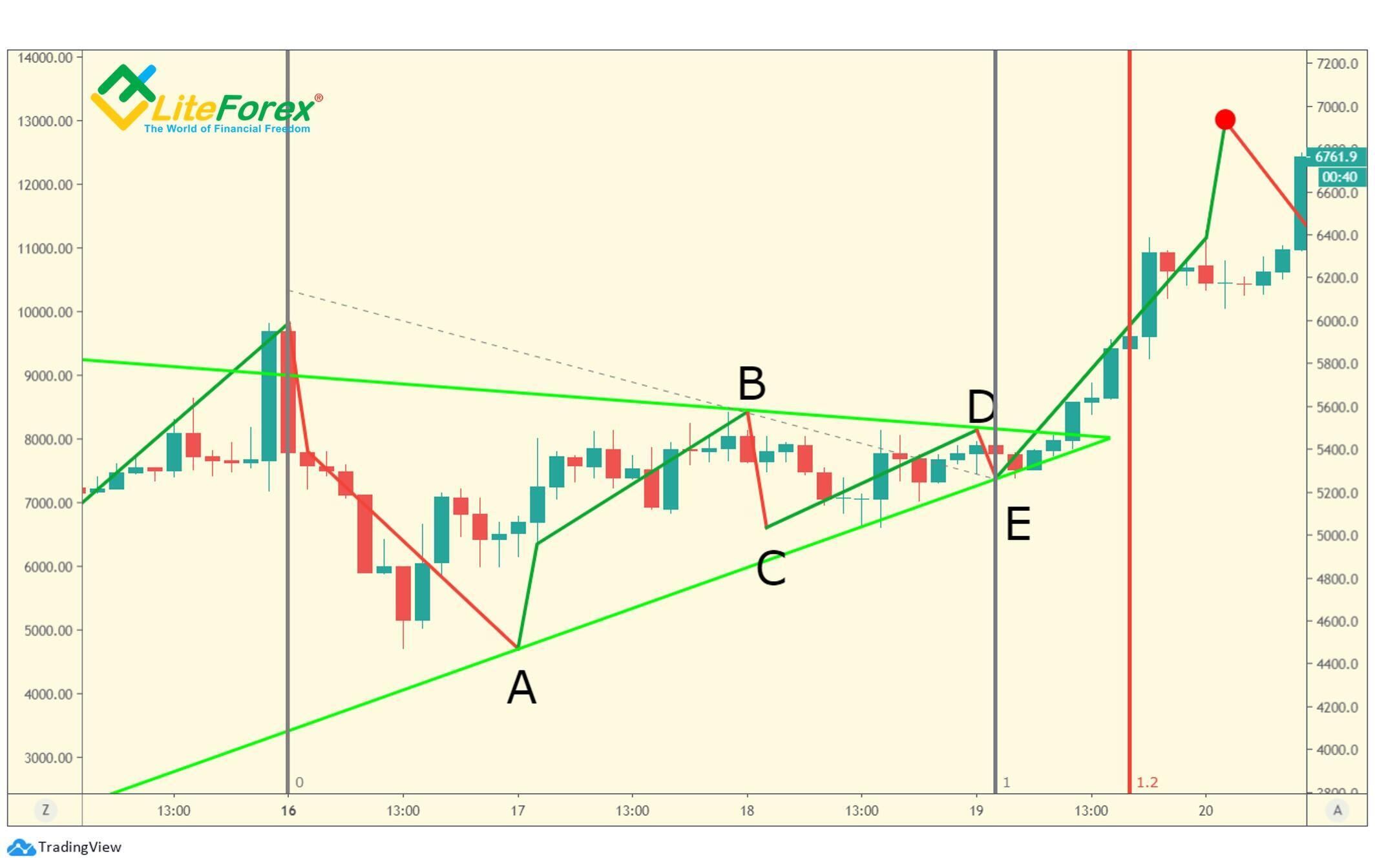
Przeanalizujmy kurczący się trójkąt na przykładzie.
Najpierw sprawdźmy, czy przestrzegane są ogólne zasady dotyczące wszystkich trójkątów.
1. Badany wzór składa się z 5 segmentów: a, b, c, d oraz e.
2. Jeśli spełnione są inne ogólne wymagania, zasada trójki zostanie spełniona w każdym przypadku, więc dzięki temu nie będziemy tracić czasu na analizowanie każdego segmentu trójkąta. W praktyce szczegółową analizę struktury segmentów zalecam tylko wtedy, gdy wahacie się odnośnie rodzaju wzoru, z którym macie do czynienia.
3. Wszystkie segmenty w trójkącie znajdują się w tym samym obszarze cenowym.
4. Trójkąt nieznacznie wznosi się w górę.
5. Z powyższego wykresu jasno wynika, że fala B znajduje się między 38,2% a 261,8% fali A.
6. Z czterech segmentów trzy z nich muszą znieść co najmniej 50% poprzedniej fali. Z powyższego wykresu jasno wynika, że znoszącymi segmentami są fale B i D. Fala D wygląda podejrzanie, ale po zmierzeniu relacji między D i B widzimy, że fala D stanowi 50% fali B.
7. Tylko cztery punkty końcowe dotykają linii kanału.
8. Linia trendu B-D nie jest przerwana przez żadną część fal C i E tego trójkąta.
Teraz sprawdźmy, czy ten wzór spełnia wymogi kurczącego się trójkąta.
1. Najszerszym segmentem w trójkącie jest fala A. Sprawdźmy zależność pchnięcia po trójkącie i fali A. Jak widać na powyższym wykresie, pchnięcie wynosi nieco więcej niż 100% fali A. Pchnięcie znajduje się zatem między 75% a 125% najszerszego segmentu w trójkącie.
2. W analizowanym przez nas potencjalnym kurczącym się trójkącie siła pchnięcia przekracza wyż i niż osiągnięte podczas powstawania trójkąta (różowa pozioma linia).
3. Nawet bez szczegółowej analizy wyraźnie widać, że ostatnia fala w trójkącie, fala E, jest najmniejszym ze wszystkich segmentów trójkąta.
W związku z tym możemy wywnioskować, że ta formacja ta jest kurczącym się trójkątem. W kolejnych przykładach nie będę już przedstawiał szczegółowo podstawowych zasad dla wszystkich trójkątów, aby się nie powtarzać. Kurczące się trójkąty są podzielone na trójkąty ograniczające i nieograniczające.
Ograniczające trójkąty
Trójkąty ograniczające często występują w czwartych falach i falach B wzorów korekcyjnych. Zakończenie fali E w tych wzorach powinno nastąpić między 20% a 40% przed wierzchołkiem trójkąta. Istnieją trzy odmiany trójkątów ograniczających:
Trójkąty poziome;
Trójkąty nieregularne;
Trójkąty bieżące.
Każda z tych odmian ma własne zasady konstrukcyjne. Omówię je poniżej.
Poziome trójkąty
Spośród Kurczących się Trójkątów najczęściej występującym jest trójkąt poziomy. Gdy rynek przestrzega poniższych zasad oznacza to, że tworzy się poziomy trójkąt:
Linie trendu trójkąta muszą poruszać się w przeciwnych kierunkach cenowych.
Wierzchołek trójkąta musi znajdować się w zakresie 61,8% najdłuższego segmentu trójkąta.
Fala D musi być mniejsza od fali C.
Fala E musi być mniejsza od fali D.
Nieregularne trójkąty
Ten rodzaj trójkąta oznacza nieco większy potencjał pchnięcia i prędkości niż trójkąt poziomy. Podlega on następującym zasadom:
- Fala B nie powinna wynosić więcej niż 261,8% fali A i zwykle będzie wynosić mniej niż 161,8%. Jednak dokładny związek Fibonacciego między falą A i falą B dowolnego trójkąta jest bardzo nietypowy.
- Fale c, d oraz e muszą być mniejsze niż poprzednia fala.
- Linie trendu Trójkąta powinny poruszać się w przeciwnych kierunkach.
Bieżące trójkąty
Ten wzór trójkąta jest najtrudniejszy do zinterpretowania, podlega poniższym zasadom:
- Fala B jest dłuższa od fali A i jest najdłuższą falą trójkąta.
- Fala C jest mniejsza od fali B.
- Fala D jest większa od fali C.
- Fala E jest mniejsza od fali D.
- Obie linie trendu będą wznosić się w górę lub opadać w dół.
- „Pchnięcie” po trójkącie będzie znacznie większe niż najszerszy segment trójkąta, czasami może wynosić 261.8%, ale nie więcej.
Nieograniczające trójkąty
Istnieje bardzo niewielka różnica między kurczącymi się nieograniczającymi trójkątami a kurczącymi się ograniczającymi trójkątami. Zastosowanie powinny mieć wszystkie zasady opisane powyżej, z wyjątkiem następujących subtelnych różnic, które odróżniają oba wzory.
Kanałowość. Nieograniczający trójkąt zachowuje się nieco inaczej przy zbieżnych liniach trendu niż trójkąt ograniczający. Zachowanie to występuje w jednej z trzech odmian:
- a. Najbardziej powszechnym i wyróżniającym działaniem nieograniczającym jest przeciążenie w punkcie wierzchołkowym zbieżnych linii trendu lub bardzo blisko nich. Zmierzcie czas, jaki potrzebny był trójkątowi od początku do końca fali E. Jeśli zbiegające się linie trendu pojawią się przed upływem 20% tego czasu (dodanego do końca fali E), mamy zgodność z powyższym stwierdzeniem.
- b. Mierząc czas od początku trójkąta do końca fali-e, jeśli punkt wierzchołkowy zbieżnych linii trendu wystąpi po upływie 40% tego czasu, należy go ponownie uznać za trójkąt nieograniczający. Jest to trudniejsze do przewidzenia, ponieważ formacja trójkąta nie jest zbyt oczywista.
- c. Jeśli korekta po pchnięciu przejdzie do strefy czasowej wierzchołka zbieżnych linii trendu, mamy trójkąt nieograniczający. Najczęstszym sposobem zniesienia korekty w stosunku do wierzchołka ostatniego trójkąta jest bardzo gwałtowne wypchnięcie z trójkąta, osiągające początkową długość ceny (w oparciu o najszerszą falę trójkąta) na długo przed pojawieniem się wierzchołka.
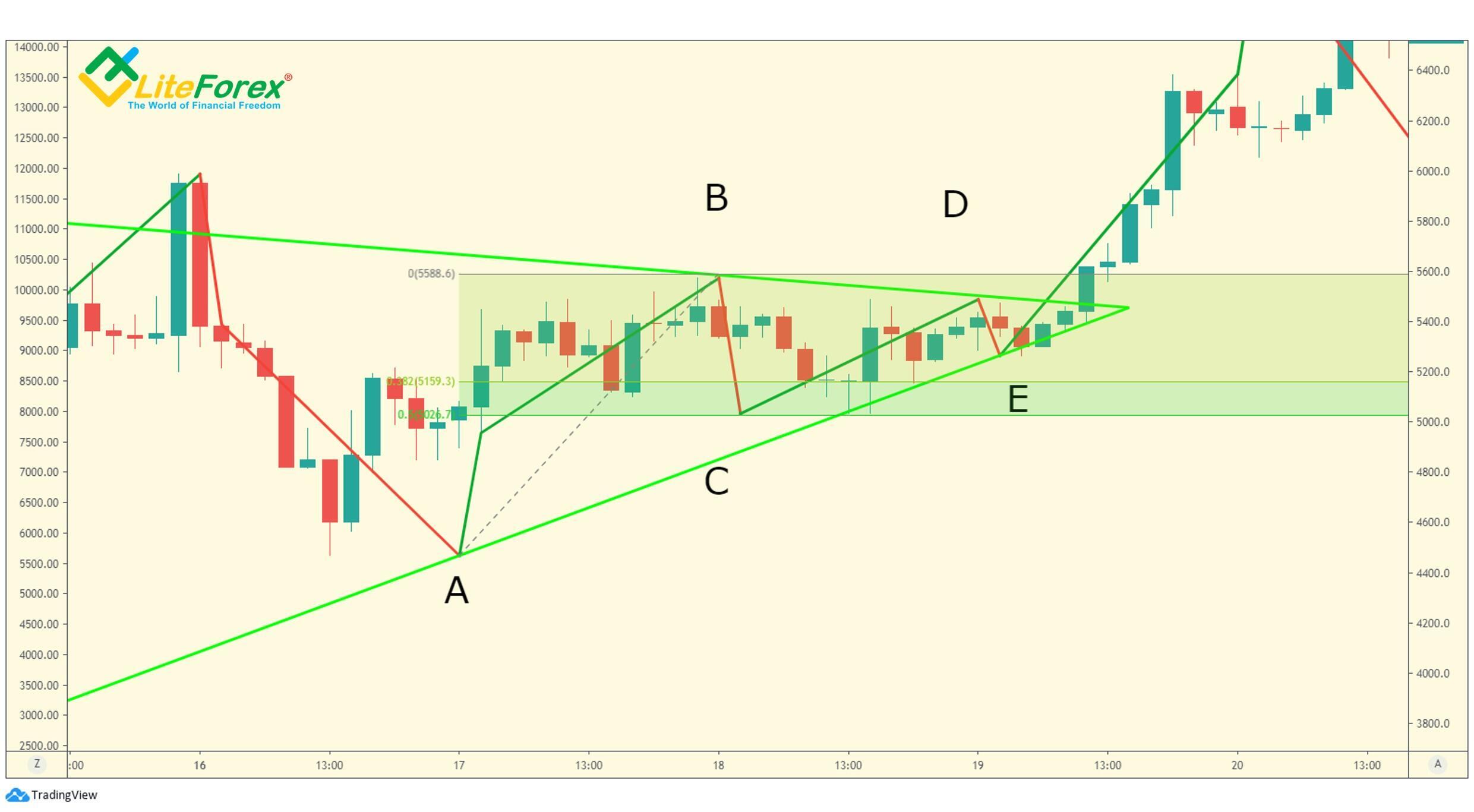
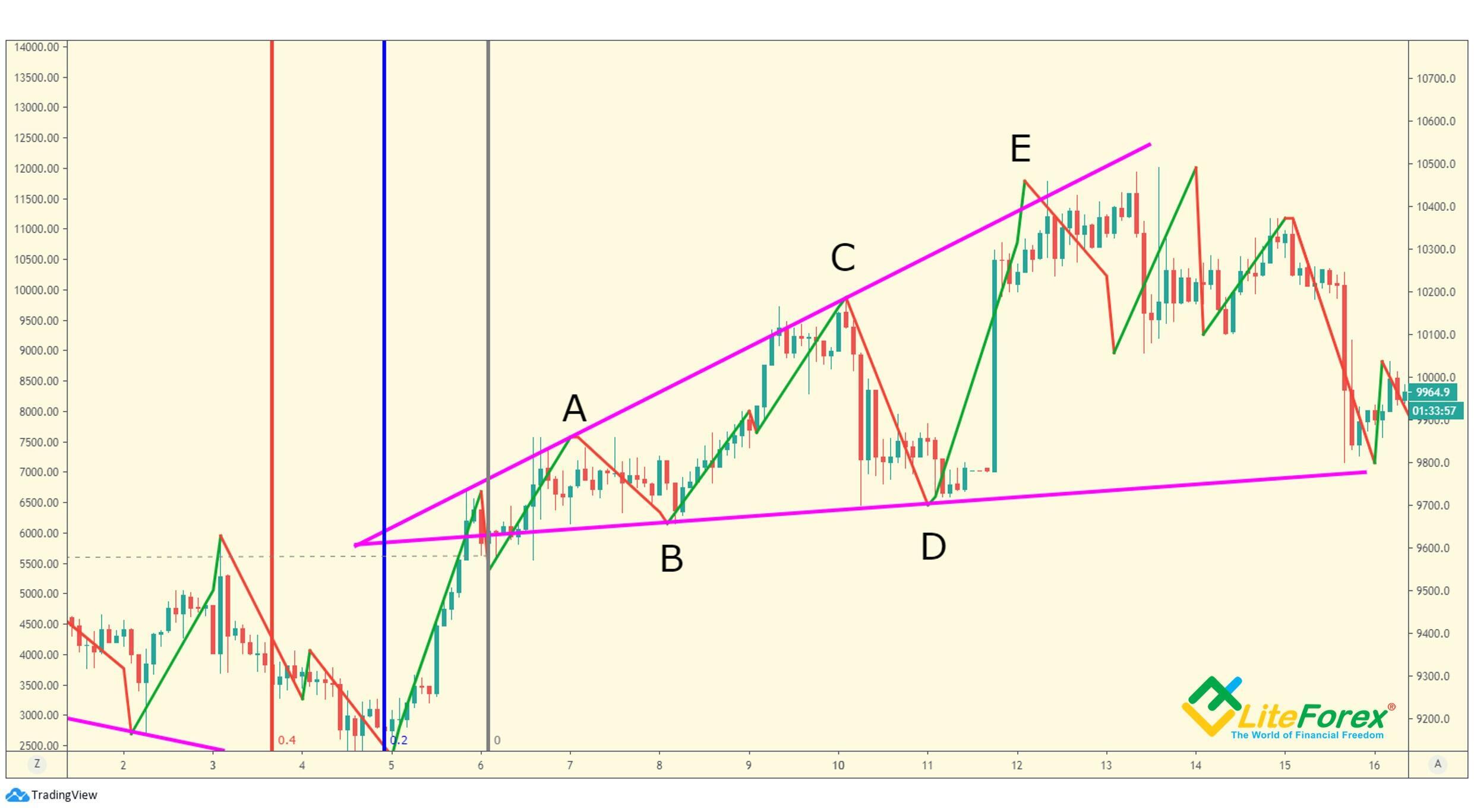
Przeanalizujmy nasz przykład i sprawdźmy jaką mamy tutaj odmianę trójkąta:
Jak widać na powyższym przykładzie, zbieżność linii trendu mierzonych od końca fali E następuje w ciągu 20% czasu, który był potrzebny trójkątowi od początku do końca fali E.
Rozszerzające się trójkąty
Rozszerzające się trójkąty występują najczęściej podczas bardzo dużych złożonych korekt. W takich wzorach większość poprzedzających segmentów obejmuje większy obszar cenowy niż poprzednie. Rozszerzające się trójkąty podlegają następującym zasadom:
- Fala A lub fala B zawsze będzie najmniejszym segmentem trójkąta.
- Fala E prawie zawsze będzie największą falą wzoru.
- Rozszerzające się trójkąty nie mogą występować jako fale B w zygzakach ani jako fale B, C lub D większego trójkąta.
- Fala E będzie zwykle najbardziej czasochłonnym i złożonym segmentem trójkąta. Najbardziej typowa konstrukcja fali E to zygzak lub złożona kombinacja korekt w większych wzorach.
- Fala E prawie zawsze wychodzi poza linię trendu przechodzącą przez górne punkty fali A i fali C.
- Linia trendu B-D powinna działać tak samo, jak w każdym kurczącym się trójkącie.
- Wypychanie z rozszerzającego się trójkąta powinno być mniejsze niż najszersza fala tego trójkąta (która w tym przypadku jest falą E), chyba że kończy silną, większą korektę.
- Trzy fale poprzedzające falę E muszą stanowić co najmniej 50% następnej fali.
Podobnie jak kurczące się trójkąty, trójkąty rozszerzające się są podzielone na dwie odrębne kategorie, trójkąty ograniczające i nieograniczające. Oba w tej formacji wskazują jedynie na to, czy trójkąt znajduje się w standardowym położeniu fali, czy jest częścią bardziej złożonej korekty, nie mają żadnych znaczących implikacji po trójkątach.
Ograniczające trójkąty
Ta odmiana rozszerzających się trójkątów jest niezwykle rzadka jako fala 4 w impulsie fali B w korekcie. Jeśli chodzi o te trójkąty, Neely ma kilka sugestii:
- Wydaje się, że rozszerzający się, ograniczający trójkąt fali B jest możliwy tylko w przypadku nieregularnej porażki lub płaskiej porażki C.
- Wypychanie z trójkąta jest minimalne, zniesienie wynosi około 61,8% trójkąta od najwyższego do najniższego punktu.
Istnieją trzy rodzaje rozszerzających się trójkątów ograniczających:
Trójkąty poziome;
Trójkąty nieregularne;
Trójkąty bieżące.
Poziome trójkąty
Poziomy rozszerzający się trójkąt jest sprzeczny z naturalną tendencją rynku do akumulacji lub dystrybucji, dlatego jest prawdopodobnie najmniej powszechną odmianą rozszerzającego się trójkąta, zwykle występuje w długich okresach czasu. Neely podaje następujące parametry w celu zidentyfikowania rozszerzającego się trójkąta.
Fala A musi być najmniejszą falą we wzorze.
Fale B, C, D oraz E muszą przekraczać punkt końcowy poprzedniego segmentu.
Fala E często wychodzi poza linię trendu poprowadzoną przez punkty końcowe fali A i B.
Nieregularne trójkąty
Nieregularny trójkąt rozszerzający się jest nieco bardziej powszechny niż poziomy i charakteryzuje się następującymi cechami:
Fala B jest mniejsza niż fala A, a wszystkie pozostałe fale są większe niż poprzednia. Lub fala D jest mniejsza niż fala C, a wszystkie inne fale są większe niż poprzednia.
Im dłuższy jest okres czasu objęty wzorem, tym bardziej prawdopodobne jest to, że kanałowanie wzoru będzie skośne, skierowane w górę lub w dół.
Bieżące trójkąty
Bieżący trójkąt często wygląda jak wzór trendu. Dzieje się tak dlatego, że spełnione są te dwa warunki:
Fala B jest nieco większa od fali A.
Fala D jest nieco krótsza niż fala C.
Poza tym linie trendu zwykle zmierzają w tym samym kierunku, choć w końcu jednak się rozchodzą. Fala E w tego rodzaju wzorze może być dość gwałtowna. Inna odmiana pojawia się wtedy, gdy wszystkie fale są większe niż poprzednia, z wyjątkiem fali C (która jest krótsza niż fala B).
Nieograniczające trójkąty
Nieograniczająca rozszerzająca się odmiana dotyczy trójkątów, które tworzą się w bardziej złożonych formacjach. Wypychanie z nieograniczającego rozszerzającego się trójkąta będzie zwykle falą X, ale może też być piątą falą wzoru końcowego lub drugą falą X w potrójnej trójce lub w potrójnej kombinacji.
Nieograniczające rozszerzające się trójkąty powstają według tych samych zasad, co ograniczające rozszerzające się trójkąty, z jednym wyjątkiem dotyczącym punktu wierzchołkowego, którym jest czas przeszły. Zmierzcie czas potrzebny całemu trójkątowi, a następnie 40% tej wartości odejmijcie od początku fali A. Wierzchołek pojawi się zanim osiągnięto 40% czasu. Zwykle pojawia się on w ciągu 20% tego czasu.
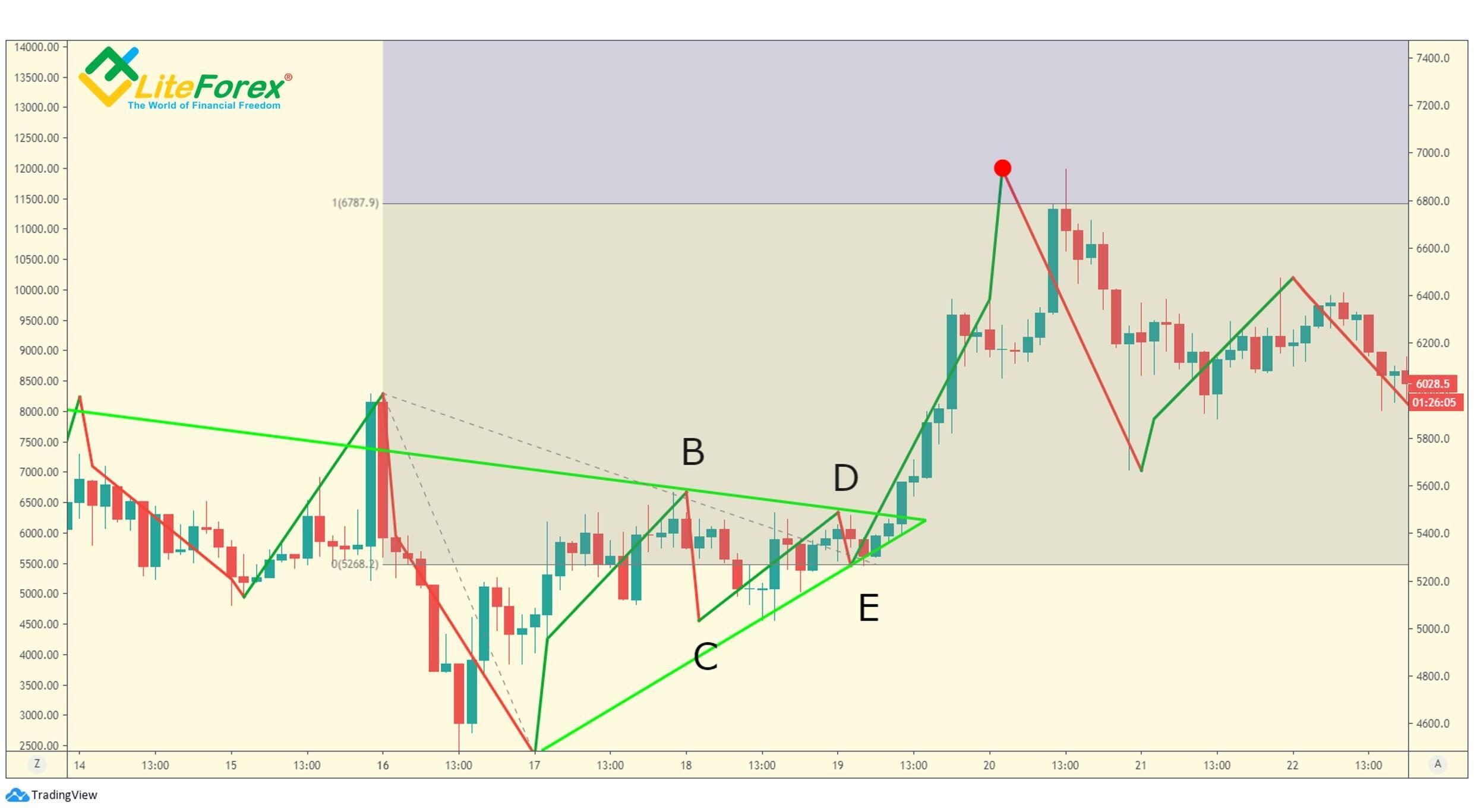
Powyższy badany trójkąt spełnia następujące ogólne zasady dotyczące trójkątów rozszerzających się:
- Fala B jest najmniejsza.
- Fala E jest największa.
- Fala E przełamuje linię trendu przechodzącą przez szczyty fali A i fali C.
- Linia trendu poprowadzona przez wierzchołki fal B i D nie jest przerwana przez żadną część fal C i E tego trójkąta.
- Wypychanie z rozszerzającego się trójkąta jest mniejsze niż najszersza fala trójkąta (czyli fala E).
- Każda z trzech fal przed falą E stanowi co najmniej 50% następnej fali.
Aby zidentyfikować odmianę rozszerzającego się trójkąta, bierzemy 20% i 40% czasu potrzebnego do powstania całego wzoru i odejmujemy segmenty od początku fali A (niebieska linia to 20% czasu, czerwona - 40%). Szczyt pojawia się przed osiągnięciem 40% czasu. A zatem mamy tutaj trójkąt nieograniczający.
To wszystko na dziś. W kolejnym artykule opiszę zasady logiki dotyczące korekt.
Dbajcie o siebie i swoje pieniądze!
Subskrybujcie mnie i czytajcie nowe artykuły jako pierwsi!
Życzę powodzenia i dużych zysków!
P.S. Podobał się mój artykuł? Udostępnij go w sieciach społecznościowych, najlepszy sposób na podziękowanie:)
Wykres cen BTCUSD w czasie rzeczywistym
Treść tego artykułu stanowi wyłącznie prywatną opinię autora i może nie pokrywać się z oficjalnym stanowiskiem LiteForex. Materiały publikowane na tej stronie mają wyłącznie charakter informacyjny i nie mogą być traktowane jako porada inwestycyjna ani konsultacja w rozumieniu dyrektywy 2014/65/UE.
Zgodnie z przepisami prawa autorskiego artykuł ten jest chronionym obiektem własności intelektualnej, co obejmuje zakaz kopiowania i rozpowszechniania bez zgody.